KREISBERECHNUNGEN

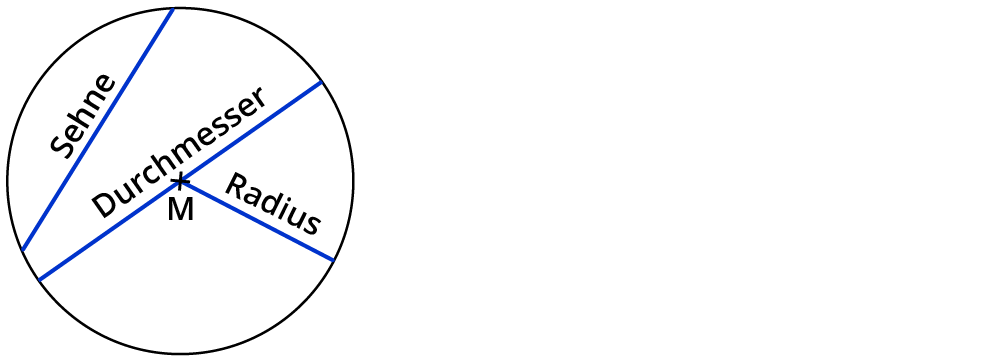
1) Berechne den Flächeninhalt der grün markierten Figur
 




 Lösung:
   

Allerdings hat man so die mit A₃ bezeichnete Fläche 2-mal subtrahiert, da sie in beiden mit A₂ bezeichneten Flächeninhalten enthalten ist; diese Fläche ist demnach 1-mal dem Ergebnis zuzuschlagen:
A=A₁-2·A₂+A₃+A₃
A=A₁-2·A₂+2·A₃

                                                                                                                                                                             

2)  Berechne den Flächeninhalt der grün markierten Figur.
 

  Lösung:
    
Die Fäche besteht aus den Teilflächen A₁, A₂ und A₃:
A₁: Sektor, Radius r, Mittelpunktswinkel 180°
A₂: Quadrat, Seitenlänge 4r
A₃: Sektor, Radius r, Mittelpunktswinkel 90°
Es gilt:
A=4·A1+A2-4·A3

                                                


3) Eine Kunststofftonne hat an der breitesten Stelle einen Umfang von 1,5 m. Wie groß ist der innere Durchmesser, wenn die Tonne eine Wandstärke von 0,5 cm hat?

Lösung:
               


4) Ein geostationärer Satellit umfliegt die Erde in einer Höhe von 36200 km. Wie schnell bewegt er sich, wenn der Erdumfang am Äquator 40074 km beträgt?

Lösung:



 


5) Bestimme den Radius eines Kreises, der den gleichen Flächeninhalt wie ein Quadrat hat, dessen Umfang 16 cm beträgt
 Lösung:





 

6)Aus einem rechteckigen Tuch mit den Maßen 1,2 m × 1,5 m wird ein möglichst großes Kreisstück geschnitten. Wie groß ist der Abfall in Prozent?
 Lösung:





                      

7)Aus einem rechteckigen Blechstück, das 5 cm breit und 7 cm lang ist, werden 35 Kreisstücke mit dem Durchmesser von 1 cm gestanzt. Berechne die Restfläche!

Lösung:
 :                             

8)Das Rad eines Eisenbahnwagens hat einen Durchmesser von 85 cm. Wie viele Umdrehungen macht das Rad in einer Stunde, wenn der Zug mit einer Geschwindigkeit von 70 km/h fährt?

Lösung:


                                         

9)

KREIS

Was ist ein Kreis?

......

Die Menge aller Punkte P, die von einem festen Punkt M die gleiche Entfernung r haben, bilden einen Kreis oder genauer eine  Kreislinie mit dem Mittelpunkt M und dem Radius r.

Ein Kreis kann auch eine Kreisscheibe sein. 
Dann ist der Kreis die Menge aller Punkte der Kreislinie und der Punkte, die sie einschließt.


 
Begriffe am Kreis 

M Mittelpunkt,  r Radius oder Halbmesser,  d Durchmesser  s Sehne

Es gibt drei verschiedene Möglichkeiten der Lagebeziehungen für eine Gerade und einen Kreis.

1. Sekante:
   Kreis und Gerade schneiden sich in genau zwei Punkten.
2. Tangente:
   Kreis und Gerade berühren sich in genau einem Punkt.
3. Passante:
   Kreis und Gerade schneiden oder berühren sich nicht
   
   
   Bedeutung der Namen: Sekante: lateinisch secare = schneiden
   Tangente: lateinisch tangere = berühren
   Passante: französisch oder italienisch passante = Vorbeigehende
   
   

Anwendungsaufgaben mit Kreisen

 

 Kreisumfang

Wenn du bei einem beliebigen Kreis den Umfang (u)
durch den Durchmesser (d) teilst, erhältst du immer die Zahl π.
Es gilt also:
π=ud
Daraus erhälst du die Umfangsformel für den Kreis.
u=π⋅d
oder wegen d=2⋅r
u=2⋅π⋅r
Hinweis: Wenn du keinen Taschenrecher mit π
-Taste hast, rechne mit π≈3,14.

Kreisfläche

Die Formel zur Berechnung des Flächeninhalts A
eines Kreises mit dem Radius r lautet:
A=π⋅r2
.
Ist nur der Durchmesser des Kreises bekannt, so musst du zunächst den Radius des Kreises berechnen, damit du die Flächenformel anwenden kannst.
r=d2

Berechnung des Radius

Der Umfang u
eines Kreises sei gegeben.
Demnach kannst du mit Hilfe der umgestellten Umfangsformel den Durchmesser d
berechnen.
d=uπ
Und mit r=d2
ergibt sich dann auch der Radius des Kreises.
Ist der Flächeninhalt eines Kreises gegeben, so berechnet man den Radius r
mit Hilfe der umgestellten Flächenformel.

A=π⋅r2

Aπ=r2

Aπ−−√=r
Der Durchmesser ergibt sich dann aus d=2r
.

Vom Umfang zum Flächeninhalt

Gegeben sei eine kreisförmige Pizza mit 128cm Umfang. Berechne den Flächeninhalt der Pizza.
1) Gegeben ist der Umfang der Pizza, und gesucht ist der Flächeninhalt.
2) Benötigte Formeln:
u=π⋅d
⇒ d=uπ,
r=d2 und A=π⋅r2
3) Rechnen: d=128cmπ≈40,74cm

r=40,74cm2≈20,37cm
A=π⋅(20,37cm)2≈1303,56cm2
4) Der Flächeninhalt der Pizza beträgt ungefähr 1303,56cm2.

Vom Flächeninhalt zum Umfang

Ein kreisförmiges Blumenbeet der Größe 25m2
soll einen Zaun bekommen. Berechne die Länge des Zauns.
1) Gegeben ist der Flächeninhalt des Beetes, und gesucht ist der Umfang.
2) Benötigte Formeln:
A=π⋅r2
⇒ r=Aπ−−√,
d=2⋅r
, u=π⋅d
3) Rechnen: r=25m2π−−−−−√≈2,82m

d=2⋅2,82m=5,64m
,
u=π⋅5,64m≈17,72m
4) Der Umfang des Beetes und damit die Länge des Zauns beträgt ungefähr 17,72m
.