Mathe Themen / Matematik Konulari: SCHNITTWINKEL

Merke!

Als Winkel zwischen einer Geraden und einer Ebene bezeichnet man den "Neigungswinkel" der Geraden auf der Ebene. Schneidet eine Gerade eine Ebene, dann gibt es logischerweise immer zwei Winkel: Einen größeren und einen kleineren. Addiert ergeben beide Winkel 180°. Als Neigungswinkel bezeichnet man von den beiden Winkeln den kleineren. Nur wenn die Gerade orthogonal (also senkrecht) zur Ebene liegt, dann erhält man zwei Winkel, die beide beide Winkel 90°, ist diesem Fall ist logischerweise auch der Winkel zwischen Gerade und Ebene 90°.

Will man den Winkel zwischen einer Geraden und einer Ebene ausrechnen, dann bietet es sich an, einfach den Normalenvektor der Ebene und den Richtungsvektor der Geraden zu wählen. Da der Normalenvektor aber orthogonal zur Ebene liegt ist der Winkel zwischen dem Richtungsvektor und dem Normalenvektor nicht gleich mit dem Winkel zwischen Gerade und Ebene. Das ist aber nicht sonderlich schlimm, denn man kann einfach 90° - (Winkel zwischen Gerade u. Normalenvektor) rechnen. Das ergibt dann den Neigungswinkel.

Winkel zwischen Gerade und Ebenennormale⇓

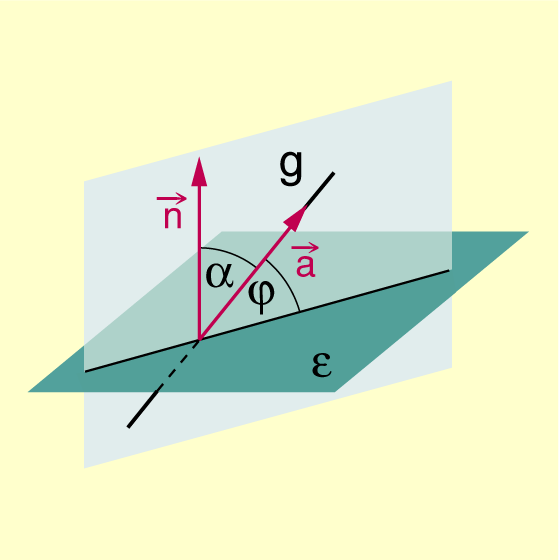Schnittwinkel einer Geraden mit einer Ebene⇓

SCHNITTWINKEL ZWISCHEN EBENE-EBENE

Merke!

Schneiden sich zwei Ebenen und soll man den Winkel zwischen diesen Ebenen errechnen, dann ist immer nach dem kleinsten Winkel gefragt (sofern nicht anders angegeben). Durch diese Regel kann der Winkel nie größer als 90° sein. Manchmal erhält man allerdings durch die Rechnung einen Winkel, der größer als 90° ist. In diesem Fall rechnet man einfach 180° minus dem errechneten Winkel. Dadurch erhält man den kleineren Winkel.