WAS IST TRIGONOMETRIE ?

Was bedeutet das Wort Trigonometrie und mit was beschäftigt sich die Trigonometrie ?

Eine kleine Information:

TRI : bedeutet   'drei'

GON : bedeutet  'Winkel ' /  ' Eck '     wie Pentagon (das Fünfeck mit fünf Winkeln )

METRIE : bedeutet  ' Messung '      wie Geometrie



Das Wort impliziert die  Dreieckwinkelmessung oder  die Dreiecksberechnung. Während Planimetrie die Konstruktion eines Dreicks aus gegebenen Stücken lehrt, bei der die Genaugkeit der Resultate verhältnismässig geringst liefert die Trigonometrie auf rechnerischem Wegexaktere Ergebnisse.

In einem rechtwinkligen Dreieck ABC seien a und b die Katheten , c die Hypothenuse die spitzen Winkel entsprechend




 
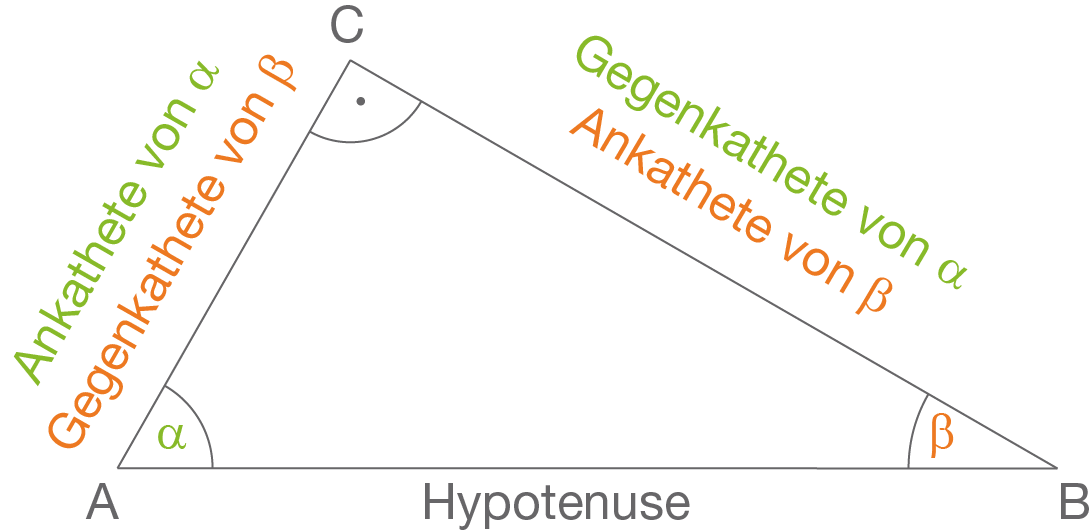
α und ß wobei gilt : α + β = 90   Man nennt a die Gegenkathete und b die Ankathete des Winkels 



Drei   Wichtige Merksätze:
1) Positive Winkel verlaufen im Gegenuhrzeigersinn
2) Mit Sin, Cos, Tan sind alle unbekannten Werte im rechtwinkligen Dreieck erreichbar. Cot ist nicht nötig.
3) Stets müssen zwei Werte bekannt sein, um den dritten Wert zu berechnen.



                                                                                                                     

             Die Seitenverhältnisse

 

Ankathete:Berührt den gemeinten Winkel

Gegenkathete:Liegt dem gemeinten Winkel gegenüber

Hypothenuse:Liegt dem rechten Winkel gegenüber

 

 Sinus :Das Seitenverhältnis Gegenkathete zu Hypothenuse

             
              G         a

sinα = ------- = -------

                 H           c

Cosinus : Das Seitenverhältnis Gegenkathete zu Hypothenuse

              A          b

 cosα = ------- = -------

              H          c

Tangens : Das Seitenverhältnis Gegenkathete zu Ankathete

              G         a
tanα = ------- = -------   

              A          b  Cotangens : Das Seitenverhältnis Ankathete zu Gegenkathete

                A           b
cotα =  -------  =  -------        
               G            a
Es gibt auch zwei Seitenverhältnisse cotangens und secans ,  die beide trigonometrische Funktionen seit längerem nicht mehr gebräuclich sind.


 Anwendung des Sinus und Cosinussatz:( gilt ein algemeines Dreieck )


Der Sinussatz kann in Dreiecken angewendet werden, bei denen


* 2 Seiten und ein nicht von ihnen eingeschlossener Winkel gegeben sind ( SSW )
* 2 Winkel in die eingeschlossener Seite gegeben sind ( WSW )

Der Cosinussatz kann in Dreiecken angewendet werden , bei denen

* 3 Seiten gegeben sind (SSS )
* 2 Seiten und der eingeschlossene Winkel gegeben sind ( WSW )
  


 
 

           Trigonometrie im Alltag

• Mit den trigonometrische Funktion die Höhe von Bäumen berechnet. Es genügt, lediglich den Winkel bis zur Baumkrone.
• Entfernungen leichter schätzen: Mit den Winkelfunktionen lassen sich tolle Dinge anstellen. Mit ihnen ist es auch möglich seinen Daumen zur Entfernungbestimmung zu benutzen.Dies kann man sich etwa beim Golfspielen zunutzemachen, um die Entfernung zum loch besser abschätzen zu können. Dazu ist es lediglich nötig, die Höhe der Fahnen zu kennen.
• Höhe von Wolken ermitteln.
• Sie Spannung in der Steckdose entsteht beispielweise auf der Grundlage einer Sinus_Funktion

Beispiel: Bestimmung der Breite eines Flusses


Zuerst wird eine Standlinie s abgesteckt. Von s aus wird ein markanter Punkt C auf den gegenüberliegenden Ufer unter dem Winkel α= 90° zur Standlinie angepeilt und so der Punkt A festgelegt. Von einem weiteren Punkt B auf der Standlinie wieder C angepeilt und der Winkel β sowie die Länge der Strecke AB gemessen. Mit diesen Daten jetzt ein maßstabgerechtes Dreieck gezeichnet und die Flussbreite b näherungsweise bestimmt werden.

EINHEITSKREIS : Der Einheitskreis ist der Kreis um den Ursprung mit Radius r= 1

             
 

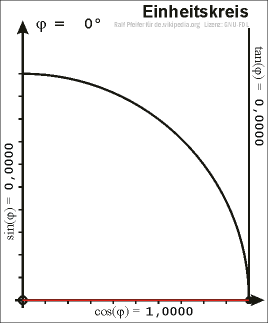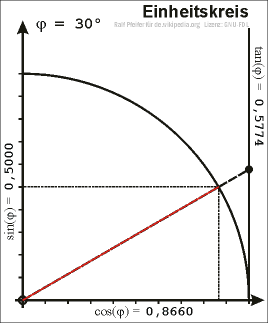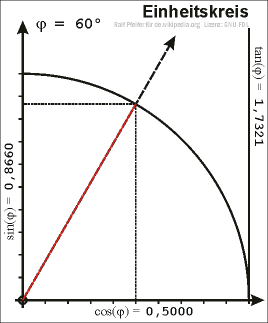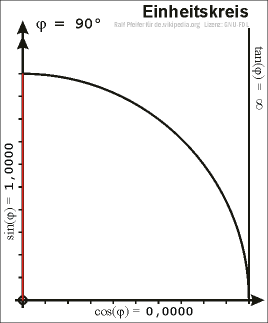
cos α= x Werte
sin α = y Werte                                                                        

 Vorzeichen des Kosinus

Vorzeichen des Sinus